Метод реализации оригинального РО-алгоритма Полларда

Генератор псевдослучайных чисел дает числа, которые оказываются не совсем случайными. Этот тезис ведет к эффек­тивному методу разложения на простые множители, открытому Дж. М. Поллардом. Число шагов вычислений в методе Полларда имеет порядок поэтому при больших N он значительно быстрее алгоритма разложения на простые множители путем деления. Среднее время выполнения алгоритма, реализующего метод Полларда, обычно меньше, чем N^1/4.

Пусть f(x) — полином с целочисленными коэффициентами. Рассмотрим две последовательности

x₀ = y₀ = A; _xm+1 = f(x_m) mod N, y_m+1 = f(_ym) mod p,

где р — любой простой множитель числа N. Тогда

y_m = x_m mod p при m ≥ 1.

Видно, что для некоторого m ≥ 1 выполняется равенство y_m = y_l(m)-1 ,где l(m) – наибольшая степень 2, но превышающая m. Таким образом, разность x_m - x_l(m)-1 будет кратна р. Далее, если f(y) mod р ведет себя как случайное отображение множества {0,1,…,р-1} на самое себя, то среднее значение наименьших из таких m будет порядка . Фактически это сред­нее значение для случайных выборок меньше 1.625Q(р)[8]; функция Q(p) .

Если различные простые делители числа N соответствуют различным значе­ниям m (что для больших N почти всегда верно), их можно найти, вычисляя gcd(x_m – x_{l(m) – 1},N) для m = 1, 2, 3, … до тех пор, пока остаток от деления на множитель не станет простым. Поллард назвал этот метод РО-методом, так как периодическая последовательность вида у₀, y₁, … напоминает греческую букву ρ.

Простейшим видом полинома является квадратичный полином f(х) = х² + 1. Нам неизвестно, обеспечивает ли данная функция случайность, но недостаток знаний по этому вопросу склоняет нас, скорее всего, в пользу гипотезы о том, что функция обеспечивает достаточную случайность, а эмпирическая проверка показала, что она ведет себя так, как и предполагалось. В действительности же функция f, вероятно, даже дает немного больше, чем случайность, так как x² + 1 содержит только ½(р + 1) различных значений по модулю р.

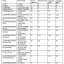
РО-алгоритм Полларда с высокой вероятностью вычисляет простые множители данного целого числа N≥2, хотя не исключен и отрицательный результат (т.е. множитель найден не будет). Рассмотрев десять наибольших простых шестиразрядных чисел, можно полу­чить лучший способ использования алгоритма Полларда. Количество итераций m(р), требуемое алгоритму Полларда для нахождения множителя р, приведено в следующей таблице.

р =      999863  999833  999907  999917  999931  999953  999959  999961  999979  999983

m(р) = 276       409        2106      1561      1593      1091      474       1819       395        814

Экспериментальным путем установлено, что среднее значение m(р) примерно равно и никогда не превышает , когда р < 1 000000. При р < 10⁶ максимум m(р) равен m(874 771) = 7685. Максимум функции m(р)/ достигается при р = 290047 и m(р) = 6251. На основании этих результатов почти все 12-разрядные числа можно разложить на простые множители быстрее чем за 2 000 итераций алгоритма Полларда (сравните с 75000 операций деления, требуемых для выполнении алгоритма разложения на простые множители путем деления).

Василенко уточнил оценку Кнута и привел ее в своей книге. ρ-метод Полларда имеет эвристическую оценку сложности O(N^1/4) арифметических операций. Покажем, как получается оценка его сложности.

Утверждение. Пусть S – фиксированное множество из r элементов, f — какое-либо отображение f: S → S, x₀ S, последовательность x₀, x₁, x₂, … определяется соотношением x_j =f (x_j-1). Пусть λ> 0, l =1 +  < r. Тогда доля тех пар(f, x₀) (где f пробегает все отображения из S в S и x₀ пробегает все множество S), у которых x₀, x₁, x₂, . ..x_l попарно различны, среди всех пар (f, x₀) не превосходит e^-λ.

Доказательство. Всего имеется r^r * r = r^r+1 различных пар (f, x₀). Пар (f, x₀), у которых x₀, x₁, x₂, . ..x_l попарно различны будет

Доля таких пар составляет величину

Поскольку при 0< x < 1 выполнено неравенство log(1 — x) < -x, то

что и требовалось доказать.

Для чего нужно доказанное утверждение? Если у n есть небольшой простой делитель p, то величина l = l(n) = 1+  имеет порядок n^1/2, в то время как величина l = l(p) =1 +  существенно меньше. А доля наборов (f, x₀ (mod n)), где f : Z/nZ → Z/nZ, у которых элементы длинного набора x₀ (mod n), … , x_l(n) (mod n) различны, не превосходит той же величины e^-λ, что и доля наборов (f, x₀ (mod p)), где f : Z/pZ → Z/pZ, у которых различны элементы короткого набора x₀ (mod p), . .. , x_l(p) (mod p).

Теорема. Пусть n—нечетное составное число, p—простой делитель n, p <, f(x)  Z[x] , x₀ Z, причем f хорошо редуцируется к модулю n, т. е. f корректно определяет отображение

f: Z/nZ → Z/nZ.

Предположим также, что f (x) хорошо редуцируется к модулю p. Если пара (f, x₀ (mod p)) является не слишком редкой по своим статистическим свойствам, то ρ-метод Полларда найдет p за O(n^1/4 log³ n) битовых операций. Точнее, существует константа c, такая, что для любого     λ > 0 вероятность не найти нетривиальный делитель n за c ·n^1/4 log³ n битовых операций будет меньше, чем e^-λ.