ProGrammer
Сайт о программировании, математике и моделировании
Объединение тестов проверки на простоту
1 Декабрь
Первым возможным улучшением предложенного теста является использование для небольших целых n > 1 в качестве оснований теста Рабина-Миллера последовательных простых чисел больших или равных 2. К примеру, доказаны следующие утверждения : Читать дальше >
Методы проверки на простоту
1 Декабрь
Все алгоритмы проверки простоты делятся на две больших подгруппы: детерминированные и вероятностные проверки. Алгоритмы первой группы позволяют точно сказать, является число простым или составным. Алгоритмы второй группы позволяют это определить, но с некоторой вероятностью ошибки. Многократное их повторение для одного числа, но с разными параметрами, обычно позволяет сделать вероятность ошибки сколь угодно малой величиной. Читать дальше >
Гипотеза Римана
1 Декабрь
Гипотеза Римана о распределении нулей дзета-функции Римана была сформулирована Бернхардом Риманом в 1859 году. Функция ζ(s) определена для всех комплексных , и имеет нули для отрицательных целых Из функционального уравнения , и явного выражения при следует, что все остальные нули, называемые «нетривиальными», расположены в полосе Читать дальше >
Китайская теорема об остатках
1 Декабрь
Пусть m – натуральное число, m1, m2, …, mt – взаимно простые натуральные числа, произведение которых больше либо равно m.
Теорема
Любое число x: 0 <= x <= m может быть однозначно представлено в виде последовательности r(x) = (r1, r2, …, rt), где ri = x(mod mi). Для любых чисел r1 .. rt, таким образом, существует единственное число x(mod m), такое что x = ri(mod mi), 1 <= i <= t Более того, любое решение x набора такого сравнений имеет вид Читать дальше >
Литература по программированию и криптографии
1 Декабрь
- Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черёмушкин А.В. Основы криптографии. М.: Гелиос АРВ, 2002. 2-е изд.
- Бондарев, Рублицкий, Качко. Основы программирования.
- Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М.:МЦНМО, 2003.—328 с.
- Василенко О.Н. Применение круговых полей в криптосистемах RSA // IV Международная конференция «Современные проблемы теории чисел и ее приложения». Тула ,10-15 сентября, 2001 /Тезисы докладов. С 36—37. Читать дальше >
Оценка ускорения РО-алгоритма
1 Декабрь
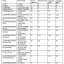
Для оценки скорости работы и ускорения алгоритма построенному с помощью различных методов была разработана программа, реализующая данные методы и проведены экспериментальные исследования. Измерения производились на Celeron 900MH, 256Mb оперативной памяти, ОС Windows XP. Читать дальше >
Ускорение РО-алгоритма с помощью алгоритма нахождения периода последовательности методом Брента.
1 Декабрь
1. [Начальная установка.] Присвоить x←5, x’←2, k←1, l←1, n←N. (Во время выполнения этого алгоритма число n не является множителем числа N, а переменные x и x’ представляют величины xm mod n xl(m)-1 mod n в выражении (1), где также f(x)=x2+1, A=2, l=l(m) и k=2l-m.)
2.1. [Проверить, будет ли число простым.] Если n – простое число Читать дальше >
Ускорение РО-алгоритма
1 Декабрь
Время на каждой итерации алгоритма Полларда, в основном, затрачивается на выполнение умножения и деления с многократной точностью и на вычисление наибольшего общего делителя. Выполнение этих операций может быть ускорено за счет применения методики «умножения Монтгомери». Читать дальше >
Реализация РО-алгоритма
1 Декабрь
РО-алгоритм Полларда
1. (Инициализация) Вводим x0, k=0;
2. k = k + 1;
3. xk = P(xk-1);
4. Если k – нечетное, идти в 2;
5.1 j = k/2.
5.2 Найти НОД (n, |xk – xj|);
6. Если НОД = 1, идти в 2;
7.1 Если НОД < n,
7.2 То p = НОД, конец;
7.3 Вывод p;
8. Если НОД делится не только на p, но и на n. Идти в 1.
Выбор среды программирования для вычислений с большими числами
1 Декабрь
В тех областях, где необходимо проводить вычисления с большими числами, важную роль играет эффективность выбора языка программирования. Оценить её можно по времени работы алгоритмов реализованных на этом языке. Предположительно, наиболее выгодно использовать языки программирования низкого уровня, в частности Ассемблер. Читать дальше >