Метод пробных делений

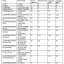
Алгоритм А (Разложение на простые множители путем деления). По данному положительному целому числу N этот алгоритм (рис. 1) находит простые множи­тели p₁ ≤ p₂ ≤ … ≤p_t, числа N в соответствии с равенством (1). В этом методе используется вспомогательная последовательность пробных делителей

2 = d₀ < d₁ < d₂ < d₃ … ,

которая включает в себя все простые числа (и, если это удобно, может сдержать числа, не являющиеся простыми). Последовательность чисел d_i должна также содержать по крайней мере одно значение, такое, что .

А1. [Начальная установка.] Присвоить t ← 0, k ← 0, n ← N. (В ходе выполнения алгоритма переменные t, k, n подчинены следующим условиям: “n = N/p₁…p_t и n не имеет простых множителей, меньших d_k”.)

А2. [n = 1?] Если n = 1, алгоритм заканчивается.

АЗ. [Разделить.] Присвоить q ← [n/d_k], r ← n mod d_k. (Здесь q и n — соответствен­но частное и остаток от деления числа n на d_k.)

А4. [Остаток равен нулю?] Если r ≠ 0, то перейти к шагу А6,

А5. [Множитель найден.] Увеличить t на 1 и присвоить p_t ← d_k, n ← q. Возвра­титься к шагу А2.

А6. [Частное мало?] Если q > d_k, увеличить k на 1 и возвратиться к шагу АЗ.

А7. [n — простое число.] Увеличить t на 1, присвоить p_t ← n и завершить выполне­ние алгоритма.