Сайт о программировании, математике и моделировании
Алгоритмы
Сложение длинных чисел
3 Декабрь
За операцию сложения отвечает процедура ADD
DIGIT Аdd(
DIGIT C[ ], // результат
const DIGIT A[ ], // первое слагаемое
const DIGIT B[ ], // второе слагаемое
int n) // длина слагаемых Читать дальше >
Умножение длинных чисел
3 Декабрь
Умножение в столбик.
С умножением дело обстоит не так просто, как с операциями сложения и вычитания. Дело в том, что известный нам со школы алгоритм умножения “в столбик” не самый быстрый. Вот он.
Алгоритм 1.3. Умножение «в столбик» длинных чисел С = А*В Читать дальше >
Разработка программы реализующей алгоритм Рабина-Миллера на С++
1 Декабрь
При выборе языка написания программы главными критериями являлись скорость выполнения и трудоемкость написания. С++ является одним из наиболее распространенных современных языков программирования. Язык С++ хорошо зарекомендовал себя эффективностью, лаконичностью записи алгоритмов, логической стойкостью программ. Ключевым понятием С++ является класс. Класс – это определяемый пользователем тип. Классы обеспечивают упрятывание данных, их инициализацию, неявное преобразование пользовательских типов, динамическое задание типов, контролируемое пользователем управление памятью и средства для перегрузки операций. В языке С++ концепции контроля типов и модульного построения программ реализованы более полно, чем в С. Кроме того, С++ содержит усовершенствования, прямо с классами не связанные: символические константы, функции-подстановки, стандартные значения параметров функций, перегрузка имен функций, операции управления свободной памятью и ссылочный тип. В С++ сохранены все возможности С эффективной работы с основными объектами, отражающими аппаратную «реальность» (разряды, байты, слова, адреса и т.д.). Это позволяет достаточно эффективно реализовывать пользовательские типы. Читать дальше >
Объединение тестов проверки на простоту
1 Декабрь
Первым возможным улучшением предложенного теста является использование для небольших целых n > 1 в качестве оснований теста Рабина-Миллера последовательных простых чисел больших или равных 2. К примеру, доказаны следующие утверждения : Читать дальше >
Методы проверки на простоту
1 Декабрь
Все алгоритмы проверки простоты делятся на две больших подгруппы: детерминированные и вероятностные проверки. Алгоритмы первой группы позволяют точно сказать, является число простым или составным. Алгоритмы второй группы позволяют это определить, но с некоторой вероятностью ошибки. Многократное их повторение для одного числа, но с разными параметрами, обычно позволяет сделать вероятность ошибки сколь угодно малой величиной. Читать дальше >
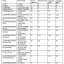
Оценка ускорения РО-алгоритма
1 Декабрь
Для оценки скорости работы и ускорения алгоритма построенному с помощью различных методов была разработана программа, реализующая данные методы и проведены экспериментальные исследования. Измерения производились на Celeron 900MH, 256Mb оперативной памяти, ОС Windows XP. Читать дальше >
Ускорение РО-алгоритма с помощью алгоритма нахождения периода последовательности методом Брента.
1 Декабрь
1. [Начальная установка.] Присвоить x←5, x’←2, k←1, l←1, n←N. (Во время выполнения этого алгоритма число n не является множителем числа N, а переменные x и x’ представляют величины xm mod n xl(m)-1 mod n в выражении (1), где также f(x)=x2+1, A=2, l=l(m) и k=2l-m.)
2.1. [Проверить, будет ли число простым.] Если n – простое число Читать дальше >
Ускорение РО-алгоритма
1 Декабрь
Время на каждой итерации алгоритма Полларда, в основном, затрачивается на выполнение умножения и деления с многократной точностью и на вычисление наибольшего общего делителя. Выполнение этих операций может быть ускорено за счет применения методики «умножения Монтгомери». Читать дальше >
Реализация РО-алгоритма
1 Декабрь
РО-алгоритм Полларда
1. (Инициализация) Вводим x0, k=0;
2. k = k + 1;
3. xk = P(xk-1);
4. Если k – нечетное, идти в 2;
5.1 j = k/2.
5.2 Найти НОД (n, |xk – xj|);
6. Если НОД = 1, идти в 2;
7.1 Если НОД < n,
7.2 То p = НОД, конец;
7.3 Вывод p;
8. Если НОД делится не только на p, но и на n. Идти в 1.
Методы ускорения алгоритмов
1 Декабрь
Первый метод ускорения заключается в том, что время вычисления НОД занимает много времени, поэтому используем китайскую теорему об остатках и попробуем ускорить начальный алгоритм. Китайская теорема об остатках: любое не отрицательное число которое не превышает каждого из множителей модуля можно однозначно восстановить если известны его остатки по этим модулям. Читать дальше >