Сайт о программировании, математике и моделировании
Записи с метками алгоритм
2. Разработка модели нарушения физической целостности информации. Часть 2. Создаем программу
31 Март
В более ранней статье мы уже рассмотрели и разработали концепцию модели оценки надежности функционирования нашей системы, следующим шагом будет разработка непосредственно программы. Программа будет реализована на языке программирования Delphi, так как, по моему мнению, при своей мощи и гибкости, язык Delphi прост в понимании и является наиболее удобным инструментом для программирования. Программы, написанные на Delphi, быстры и малы. Delphi ограждает от сложностей взаимодействия программы и компьютера, поэтому вероятность написания программы, которая займет всю доступную память компьютера, достаточно мала.
В качестве реализации модели разработана программа расчета надежности винчестера. Основное ее назначение заключается в том, что пользователь выбирает винчестер, выводятся параметры его эксплуатации, вводится температура и программа рассчитывает надежность, то есть вероятность выхода винчестера из строя и выводит сообщение о том, в порядке надежность винчестера или нет.
Реализация алгоритма вычитания длинных чисел
3 Декабрь
За операцию вычитания отвечает процедура Sub
/* Вычитание длинных чисел длины n цифр C=A-B.
В качестве результата возвращаем заем старшего разряда d */ Читать дальше >
Сложение длинного числа
3 Декабрь
Приведем реализацию алгоритма сложения, а также ввод и вывод длинного числа на Паскале.
{основная программа}
Var A, B, C : Tlong;
Begin
Assign(Input, ‘Input.txt’); Reset(Input);
ReadLong(A); ReadLong(B) ;
Close(Input);
SumLongTwo(A, B, C); Читать дальше >
Умножение длинных чисел
3 Декабрь
Умножение в столбик.
С умножением дело обстоит не так просто, как с операциями сложения и вычитания. Дело в том, что известный нам со школы алгоритм умножения “в столбик” не самый быстрый. Вот он.
Алгоритм 1.3. Умножение «в столбик» длинных чисел С = А*В Читать дальше >
Нахождение наибольшего общего делителя двух натуральных чисел
3 Декабрь
Постановка задачи:
Найти наибольший общий делитель (НОД) двух введенных натуральных чисел, используя алгоритм Евклида (алгоритм Евклида: вычитаем из большего меньшее до тех пор, пока они не сравняются, полученное в результате число и есть НОД).
Решение:
Наибольшим общим делителем (НОД) двух целых чисел называется такое наибольшее по модулю число, которое делит эти два числа. Так как натуральные числа это положительные целые числа, то при вводе двух чисел а и b должно проверяться условие, что они больше нуля. Читать дальше >
Разработка программы реализующей алгоритм Рабина-Миллера на С++
1 Декабрь
При выборе языка написания программы главными критериями являлись скорость выполнения и трудоемкость написания. С++ является одним из наиболее распространенных современных языков программирования. Язык С++ хорошо зарекомендовал себя эффективностью, лаконичностью записи алгоритмов, логической стойкостью программ. Ключевым понятием С++ является класс. Класс – это определяемый пользователем тип. Классы обеспечивают упрятывание данных, их инициализацию, неявное преобразование пользовательских типов, динамическое задание типов, контролируемое пользователем управление памятью и средства для перегрузки операций. В языке С++ концепции контроля типов и модульного построения программ реализованы более полно, чем в С. Кроме того, С++ содержит усовершенствования, прямо с классами не связанные: символические константы, функции-подстановки, стандартные значения параметров функций, перегрузка имен функций, операции управления свободной памятью и ссылочный тип. В С++ сохранены все возможности С эффективной работы с основными объектами, отражающими аппаратную «реальность» (разряды, байты, слова, адреса и т.д.). Это позволяет достаточно эффективно реализовывать пользовательские типы. Читать дальше >
Объединение тестов проверки на простоту
1 Декабрь
Первым возможным улучшением предложенного теста является использование для небольших целых n > 1 в качестве оснований теста Рабина-Миллера последовательных простых чисел больших или равных 2. К примеру, доказаны следующие утверждения : Читать дальше >
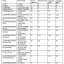
Оценка ускорения РО-алгоритма
1 Декабрь
Для оценки скорости работы и ускорения алгоритма построенному с помощью различных методов была разработана программа, реализующая данные методы и проведены экспериментальные исследования. Измерения производились на Celeron 900MH, 256Mb оперативной памяти, ОС Windows XP. Читать дальше >
Ускорение РО-алгоритма с помощью алгоритма нахождения периода последовательности методом Брента.
1 Декабрь
1. [Начальная установка.] Присвоить x←5, x’←2, k←1, l←1, n←N. (Во время выполнения этого алгоритма число n не является множителем числа N, а переменные x и x’ представляют величины xm mod n xl(m)-1 mod n в выражении (1), где также f(x)=x2+1, A=2, l=l(m) и k=2l-m.)
2.1. [Проверить, будет ли число простым.] Если n – простое число Читать дальше >
Ускорение РО-алгоритма
1 Декабрь
Время на каждой итерации алгоритма Полларда, в основном, затрачивается на выполнение умножения и деления с многократной точностью и на вычисление наибольшего общего делителя. Выполнение этих операций может быть ускорено за счет применения методики «умножения Монтгомери». Читать дальше >
