Сайт о программировании, математике и моделировании
Записи с метками сложность алгоритма
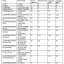
Оценка ускорения РО-алгоритма
1 Декабрь
Для оценки скорости работы и ускорения алгоритма построенному с помощью различных методов была разработана программа, реализующая данные методы и проведены экспериментальные исследования. Измерения производились на Celeron 900MH, 256Mb оперативной памяти, ОС Windows XP. Читать дальше >
Метод реализации оригинального РО-алгоритма Полларда
1 Декабрь
Генератор псевдослучайных чисел дает числа, которые оказываются не совсем случайными. Этот тезис ведет к эффективному методу разложения на простые множители, открытому Дж. М. Поллардом. Число шагов вычислений в методе Полларда имеет порядок поэтому при больших N он значительно быстрее алгоритма разложения на простые множители путем деления. Среднее время выполнения алгоритма, реализующего метод Полларда, обычно меньше, чем N1/4. Читать дальше >
Решето Эрастофена
1 Декабрь
Если известно, что N мало, резонно иметь таблицу всех необходимых простых чисел как часть программы. Например, если N меньше миллиона, то нужно включить 168 простых чисел, меньших 1000 (к этому списку нужно еще добавить значение d168 = 1000 как заключительного члена для случая, когда число N окажется простым, большим 9972). Такую таблицу можно получить при помощи короткой вспомогательной программы. Читать дальше >