Сайт о программировании, математике и моделировании
Записи с метками РО-алгоритм Полларда
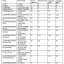
Оценка ускорения РО-алгоритма
1 Декабрь
Для оценки скорости работы и ускорения алгоритма построенному с помощью различных методов была разработана программа, реализующая данные методы и проведены экспериментальные исследования. Измерения производились на Celeron 900MH, 256Mb оперативной памяти, ОС Windows XP. Читать дальше >
Ускорение РО-алгоритма с помощью алгоритма нахождения периода последовательности методом Брента.
1 Декабрь
1. [Начальная установка.] Присвоить x←5, x’←2, k←1, l←1, n←N. (Во время выполнения этого алгоритма число n не является множителем числа N, а переменные x и x’ представляют величины xm mod n xl(m)-1 mod n в выражении (1), где также f(x)=x2+1, A=2, l=l(m) и k=2l-m.)
2.1. [Проверить, будет ли число простым.] Если n – простое число Читать дальше >
Ускорение РО-алгоритма
1 Декабрь
Время на каждой итерации алгоритма Полларда, в основном, затрачивается на выполнение умножения и деления с многократной точностью и на вычисление наибольшего общего делителя. Выполнение этих операций может быть ускорено за счет применения методики «умножения Монтгомери». Читать дальше >
Реализация РО-алгоритма
1 Декабрь
РО-алгоритм Полларда
1. (Инициализация) Вводим x0, k=0;
2. k = k + 1;
3. xk = P(xk-1);
4. Если k – нечетное, идти в 2;
5.1 j = k/2.
5.2 Найти НОД (n, |xk – xj|);
6. Если НОД = 1, идти в 2;
7.1 Если НОД < n,
7.2 То p = НОД, конец;
7.3 Вывод p;
8. Если НОД делится не только на p, но и на n. Идти в 1.
Выбор среды программирования для вычислений с большими числами
1 Декабрь
В тех областях, где необходимо проводить вычисления с большими числами, важную роль играет эффективность выбора языка программирования. Оценить её можно по времени работы алгоритмов реализованных на этом языке. Предположительно, наиболее выгодно использовать языки программирования низкого уровня, в частности Ассемблер. Читать дальше >
Метод реализации оригинального РО-алгоритма Полларда
1 Декабрь
Генератор псевдослучайных чисел дает числа, которые оказываются не совсем случайными. Этот тезис ведет к эффективному методу разложения на простые множители, открытому Дж. М. Поллардом. Число шагов вычислений в методе Полларда имеет порядок поэтому при больших N он значительно быстрее алгоритма разложения на простые множители путем деления. Среднее время выполнения алгоритма, реализующего метод Полларда, обычно меньше, чем N1/4. Читать дальше >
Решето Эрастофена
1 Декабрь
Если известно, что N мало, резонно иметь таблицу всех необходимых простых чисел как часть программы. Например, если N меньше миллиона, то нужно включить 168 простых чисел, меньших 1000 (к этому списку нужно еще добавить значение d168 = 1000 как заключительного члена для случая, когда число N окажется простым, большим 9972). Такую таблицу можно получить при помощи короткой вспомогательной программы. Читать дальше >
РО-алгоритм Полларда – алгоритм для факторизации чисел
1 Декабрь
В криптографии факторизацией называют разложение числа на простые множители. На предположении о вычисления сложности данного процесса основывается криптостойкость некоторых алгоритмов шифрования с открытым ключом, таких, как RSA, алгоритм на эллиптических кривых. Существует большое количество методов факторизации, которые отличаются вычислительной сложностью.
Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время доказано, что родственная задача о распознавании простоты числа является полиномиально разрешимой и для неё существует много эффективных тестов простоты.
Эти методы могут быть использованы в алгоритмах шифрования RSA, где вся секретная часть спрятана не в знании кода алгоритма, а в наличии ключа, длинного числа, подданного на «вход» алгоритма вместе с защищаемыми данными. Читать дальше >
